Search Results for: grow
Growth and Plant Hormones
Growth All living organisms begin in the same form: as a single cell. That cell will divide and the resulting cells will... Read More
Growth Patterns
When measuring growth, it is more desirable to use dry mass as a reliable indication. However, since you can't just 'suck'... Read More
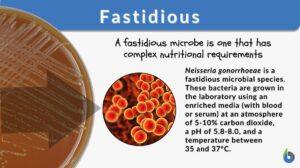
Fastidious
Fastidious Definition We can define fastidious as a term used in microbiology to denote a species that lacks the ability to... Read More
Blood Vessels Hold Key To Thicker Hair Growth
MGH researchers have succeeded in growing hair faster and thicker in mice, thanks to a protein that promotes blood vessel... Read More
Plant Meristems and Growth
A common mistake that many people assume is that an increase in size means an increase in growth. This is not the case.... Read More
Population Growth and Survivorship
By: Maria Victoria Gonzaga Previously, we learned about biodiversity and endemism. Now, let's look at the... Read More
Thermophile
Thermophiles Definition What are thermophiles? Let us first understand the literal meaning of the word ‘thermophile’.... Read More
Growth and Development of a Human Baby
Continued from the initial human reproduction of the previous page in this tutorial. Upon arrival in the uterus, the... Read More
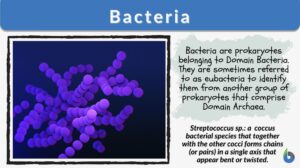
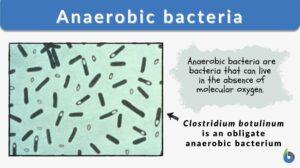
Anaerobic bacteria
Bacteria are classified according to the need for oxygen to survive and grow. For example, aerobic bacteria are bacteria... Read More
Fragmentation
Fragmentation Definition What is fragmentation? In general, fragmentation refers to the state or the process of breaking... Read More
Commensalism
Commensalism Definition What is commensalism? Literally, commensalism is a Latin word that means ‘to eat at the same... Read More
Vascular plants
Definition of Vascular plants The term 'vascular' is derived from the Latin word vāsculum, vās, meaning "a container and... Read More
Asexual reproduction
Asexual Reproduction Definition What is asexual reproduction? Asexual reproduction is a type of reproduction that does not... Read More
Unusual Plants
By Regina Bailey Plants are amazing organisms. They are able to create their own food through photosynthesis, and provide... Read More
Obligate aerobe
Before we define obligate aerobes, let us first understand and define aerobic organisms. Aerobic organisms are those that... Read More
Regeneration in humans – Finding the gene switch
Regeneration in humans is much more limited compared in other animals. Say for instance when one lost a limb, much as well... Read More
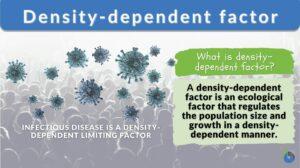
Density dependent factor
Density-dependent factors are the limiting factors of an ecosystem that regulate population growth in a density-dependent... Read More
Facultative anaerobe
Facultative Anaerobe Definition What does facultative anaerobe mean? Facultative organisms are the most adaptable... Read More
Lights’ Effect on Growth
Plants are the primary producers of energy in any ecosystem, meaning that they bring in new energy to it which supports... Read More
Susceptible
Resistance, vulnerability, sensitivity, tolerance, and susceptibility are some highly important terminologies across the... Read More
Spontaneous generation
Definition noun plural: spontaneous generations The previously popular notion that living organisms arise or develop from... Read More
Apical Dominance
a condition where vertical growth supercedes lateral growth in a plant. this is controlled by auxins, where in high... Read More
Aerotolerant
Aerotolerant Definition The term "aerotolerant" pertains to an organism that does not require oxygen for growth but can... Read More
Aerobic bacteria
Aerobic Bacteria Definition What does aerobic mean in biology? As the name suggests, 'aerobe' in biology means organisms... Read More
Apparent competition
Competition Definition One of the many branches of biology is ecology. Ecology is the study of the relationships that the... Read More