Search Results for: growth medium
Growth medium
Growth medium (Science: cell culture) a synthetic medium which is filled with nutrients necessary to the growth of... Read More
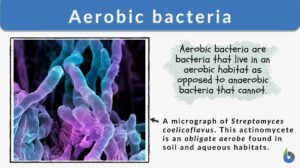
Aerobic bacteria
Aerobic Bacteria Definition What does aerobic mean in biology? As the name suggests, 'aerobe' in biology means organisms... Read More
Nutrient medium
nutrient medium --> culture medium A substance, either solid or liquid, used for the cultivation, isolation,... Read More
Growth and Plant Hormones
Growth All living organisms begin in the same form: as a single cell. That cell will divide and the resulting cells will... Read More
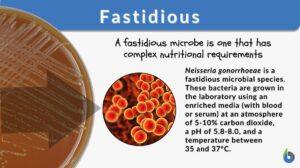
Fastidious
Fastidious Definition We can define fastidious as a term used in microbiology to denote a species that lacks the ability to... Read More
Culture medium
Culture medium a substance, either solid or liquid, used for the cultivation, isolation, identification, or storage of... Read More
Aerotolerant
Aerotolerant Definition The term "aerotolerant" pertains to an organism that does not require oxygen for growth but can... Read More
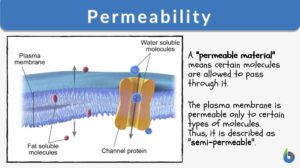
Permeability
Permeability Definition What is permeability? In earth science, its definition is this: "the ability of any material such... Read More
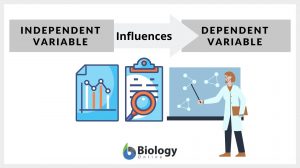
Independent variable
Independent Variable Definition To define an independent variable, let us first understand what a variable is. The word... Read More
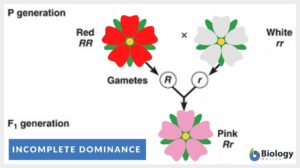
Incomplete dominance
Incomplete Dominance Definition After Gregor Mendel discovered inheritance laws, the term ''incomplete dominance'' was... Read More
The consequences of antibiotic use in horticulture
Leading articles Frederick R. Falkiner* Department of Clinical Microbiology, Trinity College, Dublin; Central Pathology... Read More
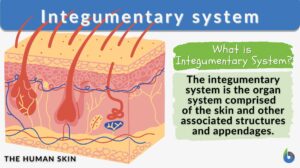
Integumentary system
Integumentary System Definition The integumentary system is the outermost layer of the body. The animal body, in... Read More
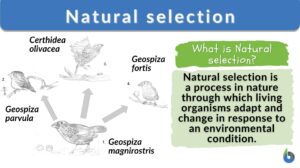
Natural selection
Natural Selection Definition What is natural selection in biology? Natural selection is defined as a process in nature... Read More
Basal medium
Basal medium (Science: cell culture) An unsupplemented medium which promotes the growth of many types of microorganisms... Read More
Hypertonic
Hypertonic Definition Hypertonic is a term used to describe an entity being in the state of hypertonicity, where there is a... Read More
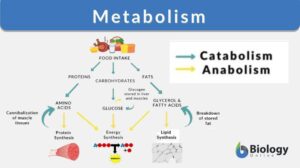
Metabolism
Metabolism Definition What is metabolism in the body? Metabolism encompasses the various biochemical processes, reactions,... Read More
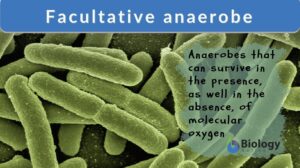
Facultative anaerobe
Facultative Anaerobe Definition What does facultative anaerobe mean? Facultative organisms are the most adaptable... Read More
Myogenesis
Definition noun (embryology) The formation of muscle tissues through the differentiation of progenitor cells myoblasts... Read More
Harvesting
Harvesting 1. (Science: cell culture) The collecting of cells, organisms, or the growth medium upon which an experimental... Read More
Turgor pressure
In biology, turgor pressure pertains to the pressure that is exerted by the fluid (e.g. water) against the cell wall. It is... Read More
Chlorophyll
Why are most plants green? Have you ever had the same question? Perhaps, you’ve been told that the plants are green... Read More
Nucleic acid
Nucleic Acid Definition A nucleic acid refers to any of the group of complex compounds consisting of chains of monomers of... Read More
Elective culture
Elective culture a method of isolating microorganisms capable of utilizing a specific substrate by incubating an inoculum in... Read More
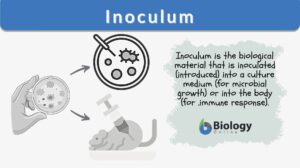
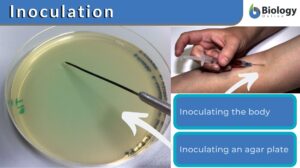
Inoculation
Inoculation Definition In Immunology, inoculation is defined as the process of introducing an antigenic substance or... Read More
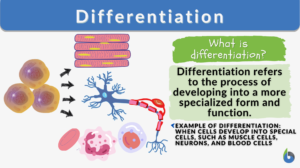
Differentiation
Differentiation in biology is the process where less specialized cells undergo changes to develop specialized structures and... Read More
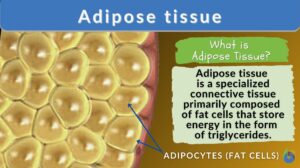
Adipose tissue
Adipose Tissue Definition Adipose tissue, a specialized variety of connective tissue, is composed of lipid-rich cells known... Read More
Cyclic adenosine monophosphate
Definition noun plural: cyclic adenosine monophosphates (biochemistry) A cyclic form of adenosine monophosphate that... Read More