Search Results for: ion pump
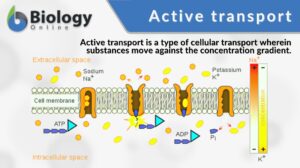
Active transport
Active transport is a type of cellular transport in which substances (e.g. ions, glucose, and amino acids) are transported... Read More
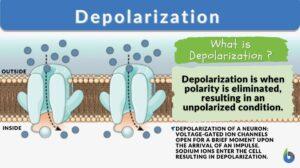
Depolarization
Depolarization is the removal of polarity by a process or action. It might also be used to describe how such activity leads... Read More
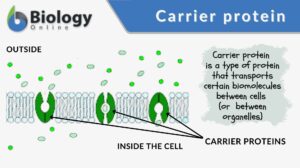
Carrier protein
Carrier protein is a type of cell membrane protein involved in facilitated diffusion and active transport of substances out... Read More
Generation of resting membrane potential
Stephen H. Wright Department of Physiology, College of Medicine, University of Arizona, Tucson, Arizona 85724... Read More
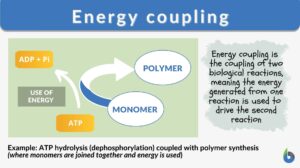
Energy coupling
What is Energy Coupling? Work, whether it be physical or biological, requires energy to be expended. In biological... Read More
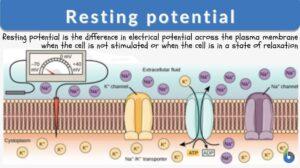
Resting potential
Resting Potential Definition The resting potential of a cell is defined as the difference in electrical potential across... Read More
Sarcoplasmic reticulum
Definition noun plural: sarcoplasmic reticula (cell biology) The special type of smooth endoplasmic reticulum found in... Read More
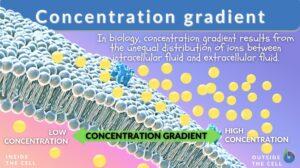
Concentration gradient
What is a concentration gradient? A gradient is a measure of how steep a slope is. Thus, a concentration gradient would be... Read More
Endoplasmic reticulum
Endoplasmic Reticulum Definition The endoplasmic reticulum is a membrane-bound organelle in cells of eukaryotic cells... Read More
ATP synthase
Definition noun, plural: ATP synthases An enzyme that catalyzes the formation of ATP from the phosphorylation of ADP with... Read More
Smooth endoplasmic reticulum
Smooth Endoplasmic Reticulum Definition Smooth endoplasmic reticulum (sER) is part of or a region in the endoplasmic... Read More
Solvent drag
Definition noun, plural: solvent drags The transportation of ultrafiltrate back from the renal tubule through the flow of... Read More
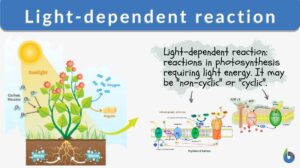
Light-dependent reaction
Many organisms, such as green plants, convert light energy into chemical energy through the mechanism of photosynthesis. In... Read More
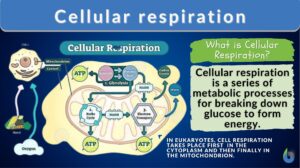
Cellular respiration
Cellular Respiration Definition What is cellular respiration in simple terms? Cellular respiration can be defined simply as... Read More
Neural Control Mechanisms
Nerve cells called neurons generate electric signals that pass from one end of the cell to another and release chemical... Read More
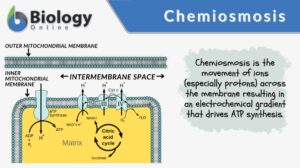
Chemiosmosis
Chemiosmosis Definition What is chemiosmosis? In biology, chemiosmosis refers to the process of moving ions (e.g. protons)... Read More
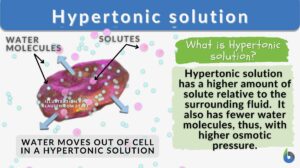
Hypertonic solution
Hypertonic Solution Definition Hypertonic solution is a relative term that describes the solution having a higher amount of... Read More
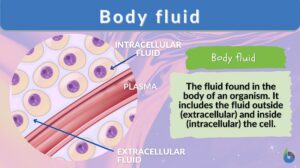
Body fluid
Body Fluids Definition What is body fluid? Literally, body fluid is the fluid of the body. The adult human body is ~50-60%... Read More
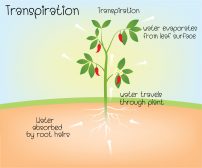
Water in Plants
The movement of molecules, specifically water and any solutes, is vital to understand in light of plant processes. This will... Read More
Aldosterone
Definition noun, plural: aldosterones A mineralocorticoid with a chemical formula of C21H28O5, and controls salt and water... Read More